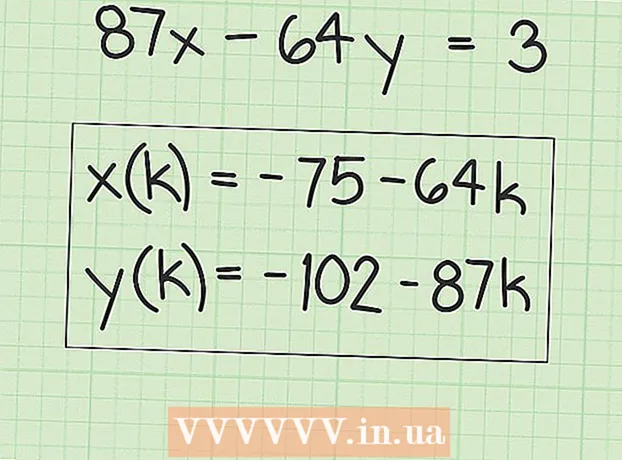
Мазмун

• Кадамдар
• 4 -жылдын 1 -бөлүгү: Теңдеме кантип жазылат
• 4 -бөлүктүн 2 -бөлүгү: Евклиддин алгоритмин кантип жазуу керек
• 4 -бөлүктүн 3 -бөлүгү: Евклид алгоритмин колдонуу менен кантип чечүү керек
• 4 ичинен 4 -бөлүк: Чексиз башка чечимдерди табыңыз

Сызыктуу Диофантин теңдемесин чечүү үчүн бүтүн сандар болгон "x" жана "y" өзгөрмөлөрүнүн маанилерин табуу керек. Бүтүн сандагы чечим адаттагыдан алда канча татаал жана белгилүү бир аракеттерди талап кылат. Биринчиден, сиз коэффициенттердин эң чоң жалпы бөлүүчүсүн (GCD) эсептеп, анан чечим табышыңыз керек. Сызыктуу теңдемеге бир бүтүн сандын чечимин тапкандан кийин, чексиз башка чечимдерди табуу үчүн жөнөкөй үлгү колдоно аласыз.

Кадамдар

4 -жылдын 1 -бөлүгү: Теңдеме кантип жазылат

1. 1 Теңдемени стандарттык түрдө жазыңыз. Сызыктуу теңдеме - өзгөрмөлөрдүн көрсөткүчтөрү 1ден ашпаган теңдеме. Мындай сызыктуу теңдемени чечүү үчүн адегенде аны стандарт түрүндө жаз. Сызыктуу теңдеменин стандарт формасы мындай көрүнөт: ${ Displaystyle Ax + By = C}$, кайда ${ Displaystyle A, B}$ жана ${ Displaystyle C}$ - Бүтүн сандар.
   • Эгерде теңдеме башка формада берилсе, аны негизги алгебралык амалдарды колдонуу менен стандарттык формага алып келиңиз. Мисалы, теңдеме берилген ${ Displaystyle 23x + 4y -7x = -3y + 15}$... Окшош терминдерди бериңиз жана теңдемени мындай жазыңыз: ${ Displaystyle 16x + 7y = 15}$.
2. 2 Теңдемени жөнөкөйлөтүңүз (мүмкүн болсо). Теңдемени стандарт түрүндө жазганда, коэффициенттерди караңыз ${ Displaystyle A, B}$ жана ${ Displaystyle C}$... Эгерде бул коэффициенттер GCDге ээ болсо, анда үч коэффициентти ага бөлүңүз. Мындай жөнөкөйлөштүрүлгөн теңдеменин чечими да баштапкы теңдеменин чечими болот.
   • Мисалы, эгер үч коэффициент тең болсо, аларды жок дегенде 2ге бөлүңүз. Мисалы:
     • ${ Displaystyle 42x + 36y = 48}$ (бардык мүчөлөр 2гө бөлүнөт)
     • ${ Displaystyle 21x + 18y = 24}$ (азыр бардык мүчөлөр 3кө бөлүнөт)
     • ${ Displaystyle 7x + 6y = 8}$ (бул теңдеме мындан ары жөнөкөйлөтүлбөйт)
3. 3 Теңдеме чечилиши мүмкүн экендигин текшериңиз. Кээ бир учурларда, теңдеменин чечимдери жок экенин дароо эле айта аласыз. Эгерде "С" коэффициенти "А" жана "В" коэффициенттеринин ГКДсына бөлүнбөсө, теңдеменин чечимдери жок.
   • Мисалы, эгер эки коэффициент тең ${ Displaystyle A}$ жана ${ Displaystyle B}$ барабар, анда коэффициент ${ Displaystyle C}$ жуп болушу керек. Бирок эгер ${ Displaystyle C}$ кызык, анда эч кандай чечим жок.
     • Теңдеме ${ Displaystyle 2x + 4y = 21}$ бүтүн чечимдер жок.
     • Теңдеме ${ Displaystyle 5x + 10y = 17}$ бүтүн чечимдер жок, анткени теңдеменин сол жагы 5ке бөлүнөт жана оң жагы жок.

4 -бөлүктүн 2 -бөлүгү: Евклиддин алгоритмин кантип жазуу керек

1. 1 Евклид алгоритмин түшүнүү. Бул мурунку калдык кийинки бөлүүчү катары колдонулган кайталанган бөлүмдөрдүн сериясы. Сандарды интегралдык түрдө бөлүүчү акыркы бөлүүчү эки сандын эң чоң жалпы бөлүүчүсү (GCD) болуп саналат.
   • Мисалы, Евклид алгоритмин колдонуп 272 жана 36 сандарынын GCDсин табалы:
     • ${ Displaystyle 272 = 7 * 36 + 20}$ - Чоң санды (272) кичирээкке (36) бөлүп, калганына (20) көңүл буруңуз;
     • ${ Displaystyle 36 = 1 * 20 + 16}$ - мурунку бөлгүчтү (36) мурунку калдыкка (20) бөлүү. Жаңы калдыкка көңүл буруңуз (16);
     • ${ Displaystyle 20 = 1 * 16 + 4}$ - мурунку бөлгүчтү (20) мурунку калдыкка (16) бөлүү. Жаңы калдыкка көңүл буруңуз (4);
     • ${ Displaystyle 16 = 4 * 4 + 0}$ - Мурунку бөлгүчтү (16) мурунку калдыкка (4) бөлүңүз. Калганы 0 болгондуктан, биз 4 баштапкы 272 жана 36 сандарынын GCD деп айта алабыз.
2. 2 Евклид алгоритмин "А" жана "В" коэффициенттерине колдонуңуз. Сызыктуу теңдемени стандарт түрүндө жазганда, "А" жана "В" коэффициенттерин аныктап, андан кийин GCD табуу үчүн аларга Евклиддин алгоритмин колдон. Мисалы, сызыктуу теңдеме берилген ${ Displaystyle 87x-64y = 3}$.
   • Бул жерде Евклиддин A = 87 жана B = 64 коэффициенттеринин алгоритми:
     • ${ Displaystyle 87 = 1 * 64 + 23}$
     • ${ Displaystyle 64 = 2 * 23 + 18}$
     • ${ Displaystyle 23 = 1 * 18 + 5}$
     • ${ Displaystyle 18 = 3 * 5 + 3}$
     • ${ Displaystyle 5 = 1 * 3 + 2}$
     • ${ Displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Эң улуу жалпы факторду (GCD) табыңыз. Акыркы бөлүүчү 1 болгондуктан, GCD 87 жана 64 1. Ошентип, 87 жана 64 бири -бирине салыштырмалуу жөнөкөй сандар.
4. 4 Жыйынтыгын талдаңыз. Gcd коэффициенттерин тапканыңызда ${ Displaystyle A}$ жана ${ Displaystyle B}$, аны коэффициент менен салыштырыңыз ${ Displaystyle C}$ баштапкы теңдеме. Эгерде ${ Displaystyle C}$ gcd менен бөлүнөт ${ Displaystyle A}$ жана ${ Displaystyle B}$, теңдемеде бүтүн сандагы чечим бар; антпесе теңдеменин чечимдери жок.
   • Мисалы, теңдеме ${ Displaystyle 87x-64y = 3}$ чечилиши мүмкүн, анткени 3 1гө бөлүнөт (gcd = 1).
   • Мисалы, GCD = 5 дейли. 3 5ке бирдей бөлүнбөйт, андыктан бул теңдеменин бүтүн сандык чечимдери жок.
   • Төмөндө көрсөтүлгөндөй, эгерде теңдемеде бир бүтүн сандык чечим болсо, анда ал дагы башка бүтүн сандык чечимдердин чексиз санына ээ.

4 -бөлүктүн 3 -бөлүгү: Евклид алгоритмин колдонуу менен кантип чечүү керек

1. 1 GCD эсептөө үчүн кадамдарды номерлөө. Сызыктуу теңдеменин чечимин табуу үчүн алмаштыруу жана жөнөкөйлөтүү процессинин негизи катары Евклид алгоритмин колдонуу керек.
   • GCD эсептөө үчүн кадамдарды номерлөө менен баштаңыз. Эсептөө процесси мындай көрүнөт:
     • ${ displaystyle { text {Step 1}}: 87 = (1 * 64) +23}$
     • ${ Displaystyle { text {2 -кадам}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {3 -кадам}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Step 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {5 -кадам}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {Step 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Step 7}}: 2 = (2 * 1) +0}$
2. 2 Калган жерде калган акыркы кадамга көңүл буруңуз. Калганын бөлүү үчүн бул кадамдын теңдемесин кайра жазыңыз.
   • Биздин мисалда, калдыктар менен акыркы кадам 6 -кадам. Калгандары 1. 6 -кадамдагы теңдемени төмөнкүдөй кайра жазгыла:
     • ${ Displaystyle 1 = 3- (1 * 2)}$
3. 3 Мурунку кадамдын калганын бөлүп коюңуз. Бул процесс этап-этабы менен "өйдө көтөрүлүү". Ар бир жолу сиз калган кадамды мурунку кадамдагы теңдемеде бөлүп аласыз.
   • 5 -кадамдагы теңдеменин калган бөлүгүн бөлүп алыңыз:
     • ${ Displaystyle 2 = 5- (1 * 3)}$ же ${ Displaystyle 2 = 5-3}$
4. 4 Жөнөкөйлөтүү жана алмаштыруу. Байкаңыз, 6 -кадамдагы теңдеме 2 санын камтыйт, ал эми 5 -кадамдагы теңдемеде 2 саны обочолонот. Ошентип, 6 -кадамдагы теңдемедеги "2" ордуна, 5 -кадамдагы сөздү алмаштырыңыз:
   • ${ Displaystyle 1 = 3-2}$ (6 -кадамдын теңдемеси)
   • ${ Displaystyle 1 = 3- (5-3)}$ (2 ордуна бир сөз айкашы алмаштырылды)
   • ${ Displaystyle 1 = 3-5 + 3}$ (ачылган кашаа)
   • ${ Displaystyle 1 = 2 (3) -5}$ (жөнөкөйлөштүрүлгөн)
5. 5 Алмаштыруу жана жөнөкөйлөтүү процессин кайталаңыз. Евклид алгоритмин тескери тартипте жылдырып, сүрөттөлгөн процессти кайталаңыз. Ар бир жолу мурунку кадамдагы теңдемени кайра жазып, сиз алган акыркы теңдемеге туташтырасыз.
   • Биз караган акыркы кадам 5 -кадам болгон. Ошентип, 4 -кадамга барыңыз жана калганын теңдемеде бөлүңүз:
     • ${ Displaystyle 3 = 18- (3 * 5)}$
   • Бул теңдөөнү "3" деген сөзгө алмаштырыңыз:
     • ${ Displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ Displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ Displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Алмаштыруу жана жөнөкөйлөтүү процессин улантыңыз. Бул процесс Евклид алгоритминин алгачкы баскычына жеткенге чейин кайталанат. Процестин максаты - чечиле турган баштапкы теңдеменин 87 жана 64 коэффициенттери менен теңдеме жазуу. Биздин мисалда:
   • ${ Displaystyle 1 = 2 (18) -7 (5)}$
   • ${ Displaystyle 1 = 2 (18) -7 (23-18)}$ (3 -кадамдагы сөздөрдү алмаштырды)
     • ${ Displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ Displaystyle 1 = 9 (18) -7 (23)}$
   • ${ Displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (2 -кадамдагы сөздөрдү алмаштырды)
     • ${ Displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ Displaystyle 1 = 9 (64) -25 (23)}$
   • ${ Displaystyle 1 = 9 (64) -25 (87-64)}$ (1 -кадамдагы сөздөрдү алмаштырды)
     • ${ Displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ Displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Алынган теңдемени баштапкы коэффициенттерге ылайык кайра жазыңыз. Евклид алгоритминин биринчи баскычына кайтып келгенде, алынган теңдемеде баштапкы теңдеменин эки коэффициенти камтылганын көрөсүз. Теңдемени кайра жазыңыз, анын шарттарынын тартиби баштапкы теңдеменин коэффициенттерине дал келет.
   • Биздин мисалда баштапкы теңдеме ${ Displaystyle 87x-64y = 3}$... Демек, пайда болгон теңдемени кайра жазыңыз, ошондо коэффициенттер бирдей болот."64" коэффициентине өзгөчө көңүл буруңуз. Баштапкы теңдемеде бул коэффициент терс, ал эми Евклид алгоритминде оң. Ошондуктан, 34 факторун терс кылуу керек. Акыркы теңдеме мындай жазылат:
     • ${ Displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Чечим табуу үчүн тиешелүү мультипликаторду колдонуңуз. Эскертүү, биздин мисалда, GCD = 1, демек акыркы теңдеме 1. Бирок баштапкы теңдеме (87x-64y) 3. Ошондуктан, акыркы теңдемедеги бардык терминдерди чечүү үчүн 3кө көбөйтүү керек:
   • ${ Displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ Displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Теңдемеге бүтүн сандагы чечимди жаз. Теңдеменин коэффициенттерине көбөйтүлгөн сандар ошол теңдеменин чечимдери.
   • Биздин мисалда, чечимди бир жуп координаттар катары жазыңыз: ${ Displaystyle (x, y) = ( - 75, -102)}$.

4 ичинен 4 -бөлүк: Чексиз башка чечимдерди табыңыз

1. 1 Чексиз чечимдер бар экенин түшүнүңүз. Эгерде сызыктуу теңдемеде бир бүтүн сандын чечими болсо, анда анын чексиз бүтүн сандарынын чечимдери болушу керек. Бул жерде тез далил (алгебралык түрдө):
   • ${ Displaystyle Ax + By = C}$
   • ${ Displaystyle A (x + B) + B (y-A) = C}$ (эгер сиз "x" ге "B" кошуп, "y" дан "A" алып салсаңыз, баштапкы теңдеменин мааниси өзгөрбөйт)
2. 2 Оригиналдуу x жана y маанилерин жазыңыз. Кийинки (чексиз) чечимдерди эсептөө шаблону сиз тапкан жалгыз чечимден башталат.
   • Биздин мисалда, чечим координаттардын бир жуп болуп саналат ${ Displaystyle (x, y) = ( - 75, -102)}$.
3. 3 "Б" факторун "х" маанисине кошуңуз. Жаңы x маанисин табуу үчүн муну кылыңыз.
   • Биздин мисалда, x = -75, жана B = -64:
     • ${ Displaystyle x = -75 + ( - 64) = - 139}$
   • Ошентип, "x" жаңы мааниси: x = -139.
4. 4 "Y" маанисинен "А" факторун алып сал. Теңдеменин мааниси өзгөрбөшү үчүн, "x" ге бир санды кошкондо, "y" дан башка санды алып салуу керек.
   • Биздин мисалда, y = -102 жана A = 87:
     • ${ Displaystyle y = -102-87 = -189}$
   • Ошентип, "y" үчүн жаңы мааниси: y = -189.
   • Координаттардын жаңы түгөйү мындай жазылат: ${ Displaystyle (x, y) = ( - 139, -189)}$.
5. 5 Чечимди текшериңиз. Жаңы координат түгөйү баштапкы теңдеменин чечими экенин текшерүү үчүн, баалуулуктарды теңдемеге туташтырыңыз.
   • ${ Displaystyle 87x-64y = 3}$
   • ${ Displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ Displaystyle 3 = 3}$
   • Теңдик аткарылгандыктан, чечим туура.
6. 6 Көптөгөн чечимдерди табуу үчүн сөздөрдү жазыңыз. "X" баалуулуктары баштапкы чечимге жана "B" факторунун каалаган эселигине барабар болот. Бул төмөнкүдөй туюнтма катары жазылышы мүмкүн:
   • x (k) = x + k (B), мында "x (k)" - "x" маанилеринин жыйындысы жана "x" - сиз тапкан "x" тин баштапкы (биринчи) мааниси.
     • Биздин мисалда:
     • ${ Displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), мында y (k)-y маанилеринин жыйындысы жана y-сиз тапкан оригиналдуу (биринчи) y мааниси.
     • Биздин мисалда:
     • ${ Displaystyle y (k) = - 102-87k}$