Мазмун

• Кадамдар
• 3 методу 1: Сызыктын теңдемесинин эңкейишин эсептөө
• Метод 2 3: Эки Пунктту колдонуп эңкейишти эсептөө
• 3 -метод 3: Дифференциалдык эсептөөнү эңкейишти эсептөө үчүн колдонуу

Жантаюу түз сызыктын абсцисса огуна болгон жантаюу бурчун мүнөздөйт (жантайышы сан жагынан бул бурчтун тангенсине барабар). Жантаюу түз сызыктын теңдемесинде бар жана ийри математикалык анализде колдонулат, мында ал дайыма функциянын туундусуна барабар. Жантайууну түшүнүүнү жеңилдетүү үчүн, ал функциянын өзгөрүү ылдамдыгына таасирин тийгизет деп элестетип көрүңүз, башкача айтканда, эңкейиштин мааниси канчалык чоң болсо, функциянын мааниси ошончолук чоң болот (көз карандысыз өзгөрмөнүн бирдей мааниси үчүн).

Кадамдар

3 методу 1: Сызыктын теңдемесинин эңкейишин эсептөө

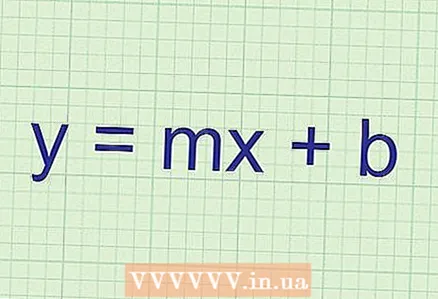1. 1 Сызыктын абсциссага болгон бурчун жана ошол сызыктын багытын табуу үчүн эңкейишти колдонуңуз. Сизге түз сызыктын теңдемеси берилсе, эңкейишти эсептөө абдан оңой. Эсиңизде болсун, ар кандай түз сызык теңдемесинде:
   • Экспоненттер жок
   • Эки гана өзгөрмө бар, алардын бири да бөлчөк эмес (мисалы, мындай ${ Displaystyle { frac {1} {x}}}$)
   • Түз сызыктын теңдемеси формага ээ ${ Displaystyle y = kx + b}$, мында k жана b сандык коэффициенттер (мисалы, 3, 10, -12, ${ displaystyle { frac {4} {3}}}$).
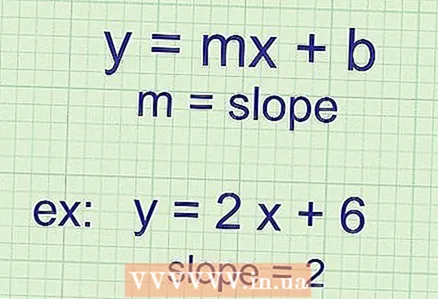2. 2 Жантайышты табуу үчүн k маанисин табуу керек ("х" коэффициенти). Эгер сизге берилген теңдеме формага ээ болсо ${ Displaystyle y = kx + b}$, андан кийин эңкейишти табуу үчүн жөн гана "x" алдындагы санды караш керек. Белгилей кетсек, k (жантайма) ар дайым көз карандысыз өзгөрмөдө болот (бул учурда "x"). Эгер түшүнбөй жатсаңыз, төмөнкү мисалдарды карап көрүңүз:
   • ${ Displaystyle y = 2x + 6}$
     • Бийиктик = 2
   • ${ Displaystyle y = 2-x}$
     • Слоп = -1
   • ${ Displaystyle y = { frac {3} {8}} x-10}$
     • Slope = ${ displaystyle { frac {3} {8}}}$
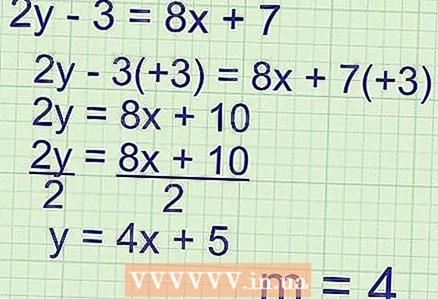3. 3 Эгер сизге берилген теңдеме башка формада болсо ж=кx+б{ Displaystyle y = kx + b}, көз каранды өзгөрмөнү изоляциялоо. Көпчүлүк учурларда, көз каранды өзгөрмө "у" деп белгиленет жана аны бөлүп кароо үчүн кошуу, азайтуу, көбөйтүү жана башка амалдарды аткарууга болот. Эсиңизде болсун, ар кандай математикалык операция теңдеменин эки тарабында тең аткарылышы керек (баштапкы маанисин өзгөртпөө үчүн). Сизге берилген бардык теңдемелерди формага алып келишиңиз керек ${ Displaystyle y = kx + b}$... Келгиле, бир мисалды карап көрөлү:
   • Теңдеменин жантаюусун табыңыз ${ Displaystyle 2y-3 = 8x + 7}$
   • Бул теңдемени формага келтирүү зарыл ${ Displaystyle y = kx + b}$:
     • ${ Displaystyle 2y-3 (+3) = 8x+7 (+3)}$
     • ${ Displaystyle 2y = 8x + 10}$
     • ${ Displaystyle { frac {2y} {2}} = { frac {8x + 10} {2}}}$
     • ${ Displaystyle y = 4x + 5}$
   • Жантыкты табуу:
     • Ийилиш = k = 4

Метод 2 3: Эки Пунктту колдонуп эңкейишти эсептөө

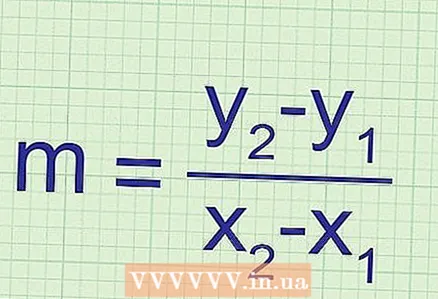1. 1 Эңкейүүнү эсептөө үчүн графикти жана эки чекитти колдонуңуз. Эгер сизге жөн гана функциянын графиги берилсе (теңдеме жок), сиз дагы жантайууну таба аласыз. Бул үчүн бул графикте каалаган эки чекиттин координаттары керек; координаттары формулага алмаштырылат: ${ Displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}}$... Эңкейүүнү эсептөөдө ката кетирбөө үчүн төмөнкүлөрдү эстен чыгарбоо керек:
   • Эгерде график өсүп жатса, анда эңкейиш оң болот.
   • Эгерде график төмөндөп жатса, анда жантаюу терс болот.
   • Напсинин мааниси канчалык жогору болсо, графа тик (жана тескерисинче).
   • Абсцисса огуна параллель түз сызыктын эңкейиши 0.
   • Ординатага параллель түз сызыктын жантаюусу жок (ал чексиз).
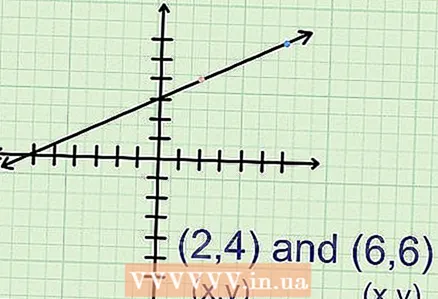2. 2 Эки чекиттин координаттарын табыңыз. Графикте каалаган эки чекитти белгилеп, алардын координаттарын табыңыз (x, y). Мисалы, графикте А (2.4) жана В (6.6) чекиттери бар.
   • Жуп координаттарда биринчи сан "x", экинчиси "y" менен дал келет.
   • Ар бир "x" мааниси белгилүү бир "y" маанисине туура келет.
3. 3 Барабар x₁, ж₁, x₂, ж₂ тиешелүү баалуулуктарга. Биздин мисалда A (2,4) жана B (6,6) пункттары менен:
   • x₁: 2
   • ж₁: 4
   • x₂: 6
   • ж₂: 6
4. 4 Табылган баалуулуктарды эңкейиш формуласына сайыңыз. Жантыкты табуу үчүн эки чекиттин координаттары колдонулат жана төмөнкү формула колдонулат: ${ Displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}}$... Эки чекиттин координаттарын сайыңыз.
   • Эки упай: А (2.4) жана В (6.6).
   • Формулага чекиттердин координаттарын алмаштырыңыз:
     • ${ Displaystyle { frac {6-4} {6-2}}}$
   • Так жооп үчүн жөнөкөйлөтүңүз:
     • ${ displaystyle { frac {2} {4}} = { frac {1} {2}}}$ = Эңкейиш
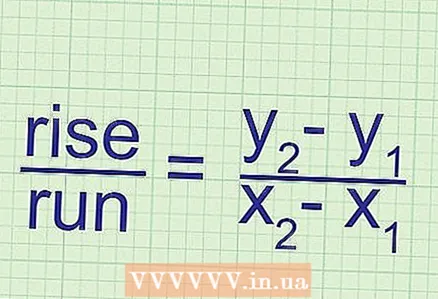5. 5 Формуланын маңызын түшүндүрүү. Жантайыш "у" координатынын өзгөрүшүнүн (эки чекит) "х" координатынын өзгөрүшүнө (эки чекит) катышына барабар. Координаттардын өзгөрүшү - бул биринчи жана экинчи чекиттердин тиешелүү координаттарынын маанилеринин ортосундагы айырма.
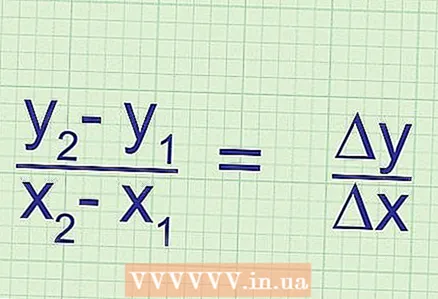6. 6 Кыймылды эсептөө үчүн формуланын дагы бир түрү. Жантайууну эсептөө үчүн стандарттык формула: k = ${ Displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}}$... Бирок ал төмөнкүдөй формада болушу мүмкүн: k = Δy / Δx, мында Δ - математиканын айырмасын билдирген грекче "дельта" тамгасы. Башкача айтканда, Δx = x_2 - x_1 жана Δy = y_2 - y_1.

3 -метод 3: Дифференциалдык эсептөөнү эңкейишти эсептөө үчүн колдонуу

1. 1 Функциялардан туундуларды алууну үйрөнүңүз. Дериватив бул функциянын графигинде жаткан белгилүү бир чекитте функциянын өзгөрүү ылдамдыгын мүнөздөйт. Бул учурда, график түз же ийри сызык болушу мүмкүн. Башкача айтканда, туунду функциянын убакыттын белгилүү бир учурундагы өзгөрүү ылдамдыгын мүнөздөйт. Туунду алынган жалпы эрежелерди эстеп, анан гана кийинки кадамга өтүңүз.
   • Туунду кантип алуу керек деген макаланы окуңуз.
   • Эң жөнөкөй туунду кантип алуу керек, мисалы, экспоненциалдык теңдеменин туундусу, бул макалада сүрөттөлгөн. Кийинки кадамдарда берилген эсептөөлөр анда сүрөттөлгөн методдорго негизделет.
2. 2 Функциянын туундусу боюнча эңишти эсептөө керек болгон маселелерди айырмалоону үйрөнүңүз. Көйгөйлөрдө функциянын жантыгын же туундусун табуу дайыма эле сунуштала бербейт. Мисалы, сизден A (x, y) чекитиндеги функциялардын өзгөрүү ылдамдыгын табууңуз суралышы мүмкүн. Сизден A (x, y) чекитиндеги жанаманын жантайышын табууңуз да суралышы мүмкүн. Эки учурда тең функциянын туундусун алуу зарыл.
   • Мисалы, функциянын жантайышын табыңыз ${ Displaystyle f (x) = 2x ^ {2} + 6x}$ пунктунда А (4.2).
   • Туунду көбүнчө катары белгилешет ${ Displaystyle f '(x), y',}$ же ${ Displaystyle { frac {dy} {dx}}}$
3. 3 Сизге берилген функциянын туундусун алыңыз. Бул жерде графикти түзүүнүн кереги жок - сизге функция теңдемеси гана керек. Биздин мисалда, функциянын туундусун алыңыз ${ Displaystyle f (x) = 2x ^ {2} + 6x}$... Жогоруда айтылган макалада айтылган методдорго ылайык туунду алыңыз:
   • Туунду: ${ Displaystyle f '(x) = 4x + 6}$
4. 4 Жантыкты эсептөө үчүн берилген чекиттин координаттарын алынган туунду менен алмаштырыңыз. Функциянын туундусу белгилүү бир учурда жантайууга барабар. Башкача айтканда, f '(x) - каалаган убакта (x, f (x)) функциясынын жантайышы. Биздин мисалда:
   • Функциянын жантайышын табыңыз ${ Displaystyle f (x) = 2x ^ {2} + 6x}$ пунктунда А (4.2).
   • Функциянын туундусу:
     • ${ Displaystyle f '(x) = 4x + 6}$
   • Бул чекиттин х-координаты үчүн маанини алмаштырыңыз:
     • ${ Displaystyle f '(x) = 4 (4) +6}$
   • Жантыкты табыңыз:
   • Функциянын жантайышы ${ Displaystyle f (x) = 2x ^ {2} + 6x}$ А (4.2) чекитинде 22.
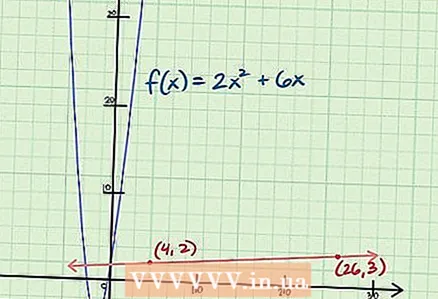5. 5 Мүмкүн болсо, жоопту графиктен текшериңиз. Эскирбеңиз, ар бир учурда эсептөө мүмкүн эмес. Дифференциалдык эсептөө татаал функцияларды жана татаал графиктерди карайт, мында эңкейиш ар бир чекитте эсептелбейт, кээ бир учурларда чекиттер графиктерде такыр жатпайт. Мүмкүн болсо, сизге берилген функция үчүн эңкейиш туура эсептелип жатканын текшерүү үчүн графикалык эсептегичти колдонуңуз.Болбосо, берилген жерге графикке тангенс тартып, сиз тапкан эңиштин мааниси графикте көргөнүңүзгө дал келеби же жокпу, карап көрүңүз.
   • Тангенс белгилүү бир чекитте функциянын графигине окшош эңкейишке ээ болот. Берилген чекитке тангенс тартуу үчүн, X огу боюнча оңго / солго жылуу (биздин мисалда оңго карай 22 баалуулук), анан Y огу боюнча бир бирдикти өйдө көтөрүңүз. Чекитти белгилеңиз , анан аны сизге берилген чекитке туташтырыңыз. Биздин мисалда, (4,2) жана (26,3) координаттарындагы чекиттерди туташтыргыла.