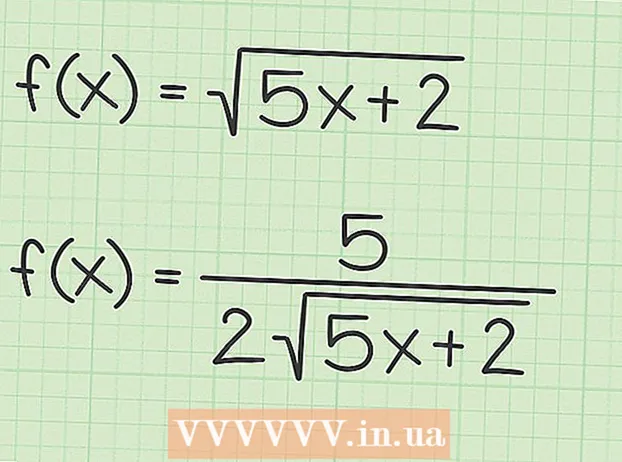
Эгер сиз мектепте математиканы окуган болсоңуз, анда жөнөкөй функциялардын туундусун аныктоочу күч эрежесин үйрөнгөнүңүз шексиз. Бирок, функцияда төрт бурчтуу тамыр же квадрат тамыр тамгасы болгондо, мисалы 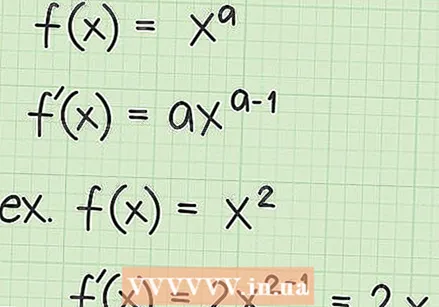${ displaystyle { sqrt {x}}}$Туундулар үчүн кубаттуулук эрежесин карап чыгыңыз. Туунду издөө боюнча сиз үйрөнгөн биринчи эреже - бул бийлик эрежеси. Бул сап өзгөрмө үчүн мындай дейт ${ displaystyle x}$Квадрат тамырын экспонент катары кайра жазыңыз. Квадрат тамыры функциясынын туундусун табуу үчүн, сандын же өзгөрүлмө чарчы тамырын көрсөткүч катарында да жазууга болорун унутпа. Тамыр белгисинин астындагы термин негиз катары жазылып, 1/2 деңгээлине чейин көтөрүлдү. Термин төрт бурчтуу тамырдын көрсөткүчү катары да колдонулат. Төмөнкү мисалдарды карап көрүңүз:

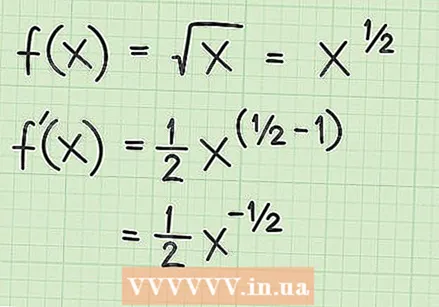• ${ displaystyle { sqrt {x}} = x ^ { frac {1} {2}}}$Кубат эрежесин колдонуңуз. Эгерде функция эң жөнөкөй квадрат тамыр болсо, 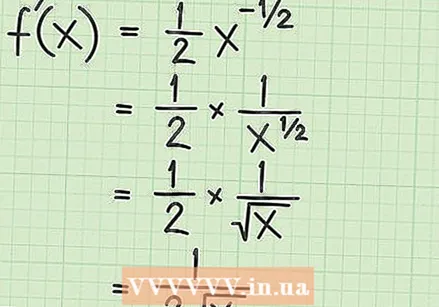${ displaystyle f (x) = { sqrt {x}}}$Натыйжаны жөнөкөйлөтүү. Бул этапта, терс көрсөткүч оң көрсөткүч менен сан кандайча болорун тескерисинче алуу дегенди билишиңиз керек. Экспоненти 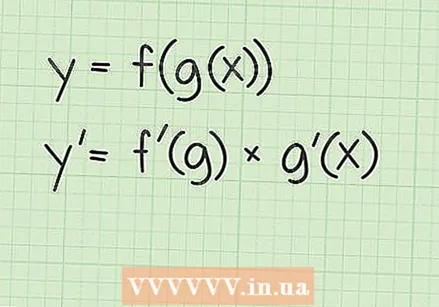${ displaystyle - { frac {1} {2}}}$Функциялар үчүн чынжыр эрежесин карап чыгыңыз. Чынжыр эрежеси - бул баштапкы функция функцияны башка функцияга бириктиргенде колдонулган туундулар үчүн эреже. Чынжыр эрежеси мындай дейт: эки функция үчүн ${ displaystyle f (x)}$Чынжыр эрежеси боюнча функцияларды аныктаңыз. Чынжыр эрежесин колдонуу сизден биринчи айкалышкан функцияны түзгөн эки функцияны аныктоону талап кылат. 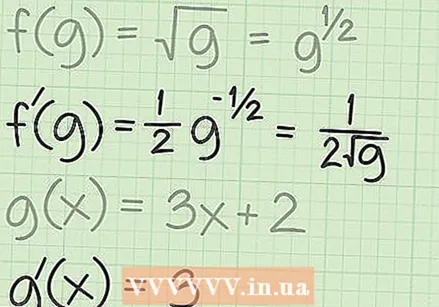Квадраттык тамыр функциялары үчүн тышкы функция ${ displaystyle f (g)}$Эки функциянын туундуларын аныктайт. Функциянын квадрат тамырына чынжыр эрежесин колдонуу үчүн, адегенде жалпы квадрат тамыр функциясынын туундусун табуу керек:
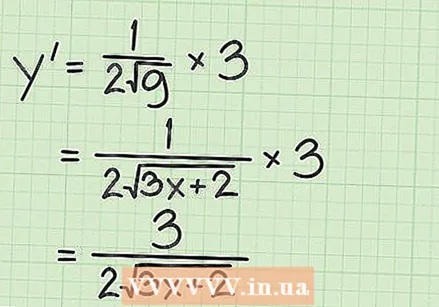  • ${ displaystyle f (g) = { sqrt {g}} = g ^ { frac {1} {2}}}$Чынжыр эрежесиндеги функцияларды айкалыштыр. Чынжыр эрежеси ${ displaystyle y ^ { prime} = f ^ { prime} (g) * g ^ { prime} (x)}$Тез ыкманын жардамы менен тамыр функциясынын туундуларын аныктаңыз. Өзгөрмөчүнүн же функциянын квадраттык тамырынын туундусун табууну кааласаңыз, жөнөкөй эрежени колдонсоңуз болот: туунду ар дайым чарчы тамырдын астындагы сандын туундусу болуп, эки эселенген баштапкы чарчы тамырга бөлүнөт. Символикалык түрдө муну төмөнкүчө чагылдырууга болот:
    • Эгерде ${ displaystyle f (x) = { sqrt {u}}}$Квадрат тамыры белгисинин астындагы сандын туундусун табыңыз. Бул төрт бурчтуу тамыр тамгасынын астындагы сан же функция. Бул тез ыкманы колдонуу үчүн, чарчы тамыр тамгасынын астындагы сандын гана туундусун табыңыз. Төмөнкү мисалдарды карап көрөлү:
      • Кызматта ${ displaystyle { sqrt {5x + 2}}}$Квадрат тамыры санынын туундусун бөлчөк санына жаз. Түбір функциясынын туундусу бөлчөк камтыйт. Бул бөлчөктүн нумератору квадраттык тамыр номеринин туундусу болуп саналат. Демек, жогоруда келтирилген функциялардын мисалында, туундунун биринчи бөлүгү төмөнкүдөй болот:
        • Эгерде 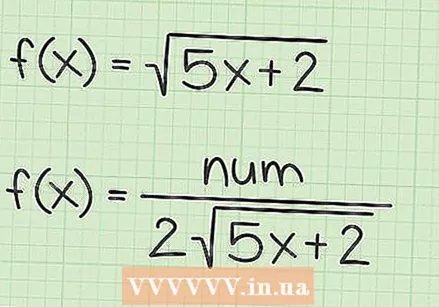${ displaystyle f (x) = { sqrt {5x + 2}}}$Бөлүштүрдү эки эселенген баштапкы квадрат тамыры менен жазыңыз. Ушул тез ыкма менен бөлүүчү баштапкы квадрат тамыр функциясынан эки эсе жогору. Демек, жогорудагы үч мисалдын функцияларында туундулардын бөлүндүлөрү:
          • Эгерде ${ displaystyle f (x) = { sqrt {5x + 2}}}$Туунду табыш үчүн, бөлгүчтү жана бөлүүчүнү бириктир. Бөлчүктүн эки жарымын бириктирип, жыйынтыгы баштапкы функциянын туундусу болот.
            • Эгерде ${ displaystyle f (x) = { sqrt {5x + 2}}}$, караганда ${ displaystyle f ^ { prime} (x) = { frac {5} {2 { sqrt {5x + 2}}}}}$
            • Эгерде ${ displaystyle f (x) = { sqrt {3x ^ {4}}}}$, караганда ${ displaystyle f ^ { prime} (x) = { frac {12x ^ {3}} {2 { sqrt {3x ^ {4}}}}}}$
            • Эгерде ${ displaystyle f (x) = { sqrt { sin (x)}}}$, караганда ${ displaystyle f ^ { prime} (x) = { frac { cos (x)} {2 { sqrt { sin (x)}}}}}$